A fast Coset Solver

To show that God's number is 20 we have to show for 55,882,296 H-cosets, each coset containing 19,508,428,800 positions, that all these positions can be solved within 20 moves.

We are able to solve each coset within 20 seconds on average, that is about 1 billion positions per second! This speed is absolutely crucial for our proof and we describe the method to achieve this in more detail in this section.

Let us take for example the H-coset which contains the well known "cube-in-the-cube" pattern r

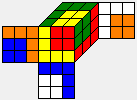
r is the representative of the coset H*r, which can be visualized after relabeling the r position as

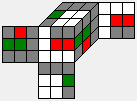
Phase 1 of the Two-Phase-Algorithm searches maneuvers m of increasing length which transform r into an H-position. Here are the first 6 maneuvers found, together with the resulting H-positions and the positions m' (the inverse of m):

Phase-1 maneuver m	Resulting H-position r*m	Position m'
U R B' R' D2 F2 D' R' B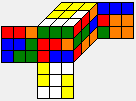
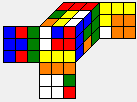U R B' R' D2 F2 D' R' B'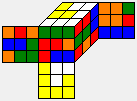
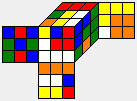U F' L2 D R' D2 F' D2 B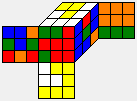
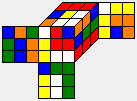U F' L2 D R' D2 F' D2 B'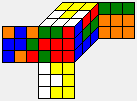
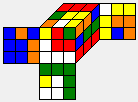U F' L2 D R' D2 B' L2 F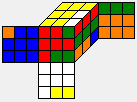
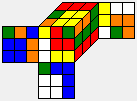U F' L2 D R' D2 B' L2 F'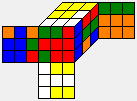

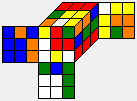Have a closer look at the positions m'. If you relabel them you will get exactly the H*r coset visualization. This means that they are all elements of the coset H*r and if you apply the maneuver m to them the result is the solved cube.
We solved 6 cubes of the coset H*r within 9 moves!

This is the first key idea of the coset solver: Taking a position r, we perform a phase1 IDA* search. Every new H-position found by a maneuver m of length N corresponds to the solve of a a position in the coset H*r of length N.

We show this more formally:

If we have found a maneuver m with r*m = h (with h from H) we have (h'*r)*m = Id, and because the inverse h' of h also is from H the position (h'*r) is from the coset H*r and is solved by the maneuver m.

h1'*r = h2'*r is equivalent to h1=h2, so the mapping f from H -> H*r : f(h) = h'*r is one to one. This means if we have "visited" all elements of H by the phase 1 search applied to position r with maneuvers with length <=N, we also have shown that all elements of the coset H*r can be solved within N moves.

The time do do a full IDA* search grows exponentially with the maneuver length N. It is not possible to do a full search even to depth 16 within a reasonable time for the 55,882,296 H-cosets. We only do a full depth 15 IDA*-search and use a bitvector of dimension 19,508,428,800 to mark all visited H-positions.

This means that at this point we solved exactly those positions of the coset H*r which do not need more than 15 moves. The time for this task is about 1.9 s per coset with the reference hardware used (Nehalem X3460 CPU running at 2.8GHz with four cores and hyperthreading enabled). Our IDA* implementation visits about 25,000,000 positions/second and uses a pruning table of size 680 MB.

If we append any move from A=<U,U2,U',D,D2,D',R2,F2,L2,B2> to an H-position, we get a different H-position. This is the second key idea of our coset solver: If we append all moves from A to all positions marked already as visited in the depth 15 bitvector, we visit a lot of new H-positions, all reachable within 16 moves.

We store all these positions together with the old ones in a new depth 16 bitvector. We call this operation a prepass; our implementation takes 3.1 s for a single prepass. Achieving this speed is anything but trivial and requires careful organization of the bitvector.We repeat this prepass 4 more times to get a depth 20 bitvector.

At this point we have solved all positions of the coset H*r where the solving maneuver has a maximum of 15 arbitrary moves followed by a maximum of 5 moves from A. The total computation time at this point is about 17.4 s for one coset.

Usually there still are a few bits not set in the bitvector, around a few hundred on average. If a bit for the H-position h still is 0, this means that we still have not solved the H*r-coset position (h'*r). All these positions can be solved individually with a Two-Phase-Algorithm solver within 20 moves.

At this point we have finally solved the complete H*r coset within 20 moves, total time is about 20 s on average.

The above description is a bit simplified. For a fraction of "difficult" cosets there are too many individual positions left at the end. For these it is better do proceed in the following way:

Full depth 15 IDA* search
Prepass
Partial depth 16 IDA* search
Four prepasses
Two-Phase-Algorithm for the remaining positions of H*r

The computation time - donated by Google - for all 55,882,296 H-cosets was about 35 CPU-years.