Solving a reduced set cover problem

With the current hard- and software the set cover problem with 138,639,780 sets is too large to be handled.

The idea is to group H-cosets together into bigger sets, so that the set cover problem has a much smaller size. This can be done in a in a natural way by introducing two new subgroups K and T, closely related to the subgroups H and Q.

Subgroup	Color Pattern	Number of Elements	Symmetry Type Symmetries
H		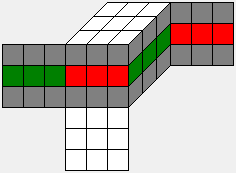\|H\| = 8! * 8! * 4! / 2 = 19,508,428,800	D4h 16
Q		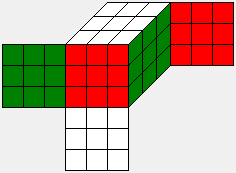\|Q\| = 4! * 4! * 4! * 4! * 4! / 2 = 3,981,312 = \|H\| / 4900	Oh 48
K		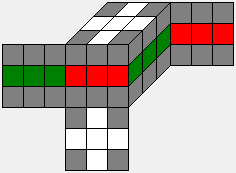\|K\| = 8! * 8! * 4! * 3⁷ / 2 = 42,664,933,785,600 = \|H\| * 2187	D4h 16
T		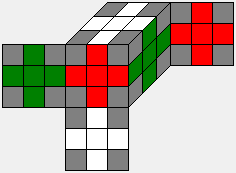\|T\| = 4! * 4! * 4! * 8! * 3⁷ / 2 = 609,499,054,080 = \|K\| / 70	Oh 48

The subgroup K can be described as the union of 2187 cosets of H having all possible 2187 corner orientations while the edges have the same properties as in the subgroup H.
The subgroup T derives likewise from the subgroup Q by dropping the restrictions on the corners. It is the union of C(8,4) * 2187 cosets of Q.

Now we list the properties of the corresponding cosets

Cosets of	Coset Example	Number of Cosets	Symmetry-reduced number
H		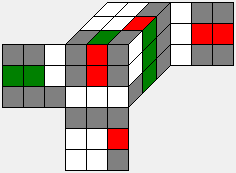[G:H] = C(12,4) * 3⁷* 2¹¹ = 2,217,093,120	138,639,780
Q		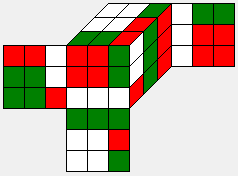[G:Q] = C(12,4) * C(8,4)² * 3⁷ * 2¹¹ = 10,863,756,288,000 = [G:H] * 4900	226,331,259,372
K		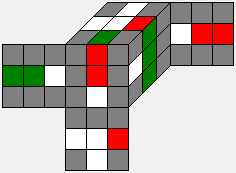[G:K] = C(12,4) * 2¹¹ = 1,013,760 =[G:H] / 2187	64,430
T		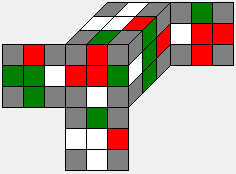[G:T] = C(12,4) * C(8,4) * 2¹¹ = 70,963,200 = [G:K] * 70	1,482,170

There are C(12,4) ways to position the red-green edges and 2^11 ways to flip the 12 edges which gives the number 1,013,760 of different K-cosets. The number of essentially different cosets reduced by the 16 D4h symmetries can be shown to be 64,430.

There are C(12,4) ways to set the position of the red-green edges and C(8,4) ways to set the position of the white-green edges, thus forcing the position of the white-red edges. There are 2^11 ways to flip the edges, so we have 495*70*2048 = 70,963,200 T-cosets. The number of essentially different T-cosets reduced by the 48 Oh symmetries can be shown to be 1,482,170.

It is important to observe that each coset of K splits into 70 cosets of T. If you take a look at the pattern example of a coset from K in the table above, there are 8 white edge facelets with the other edge facelet still grey. So you have C(8,4) ways to set the 4 missing red edge facelets and you have no choice left for the missing 4 green edge facelets.

The reduced set cover problem can be formulated in the following way:

Find a subset S of the 64430 essentially different K-cosets, each of them containing 70 T-cosets, such that all all 1,482,170 essentially different T-cosets are covered, in the sense that for each T-coset t there exists a symmetry m of Oh and a K-coset k of the subset S such that the coset m' * t * m (which is equivalent up to symmetry to t) is contained in k.

Each of the K-cosets splits again into 2187 H-cosets, and almost all of these H-cosets have to be solved to cover the whole cube space. Why not all 2187 H-cosets in all cases? This happens if the coset K has a D4h symmetry itself. Take for example the identity K-coset, which is the just the subgroup K itself. It has 16 symmetries, so there are up to 16 different H-cosets which are equivalent to each other.

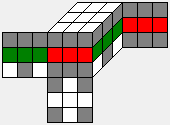
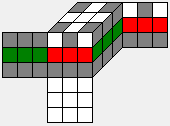
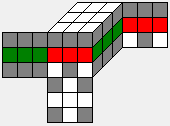
All these H-cosets are in the same equivalence class for example.

With a randomized greedy algorithm the set cover problem could be solved with 25998 K-cosets. Representatives of all cosets are here. The number of H-cosets derived from these is a bit smaller than 25998*2187 for the reasons discussed above; it is exactly 55,882,296.