The Subgroup H and its cosets
The subgroup H plays an important role in the two-phase algorithm. It is the goal state of the first phase and from there the cube is solved in the second phase.
It plays a key role in establishing God's number because we divide the whole cube space with its 43,252,003,274,489,856,000 possible cube configurations into 2,217,093,120 cosets of the subgroup H, each containing 19,508,428,800 configurations.
We choose this approach because we are able to solve every element of an H-coset with at most 20 moves at a speed of about 1,000,000,000 cubes per second (2010 PC hardware) by a method closely related to the first phase of the two-phase algorithm. This speed is a crucial feature because it allows us to essentially solve all possible cube positions within an acceptable time.
The subgroup H and its cosets can be nicely visualized if we relabel the cube in a certain way, temporarily changing the colors of the cube facelets.
If we relabel a clean cube in the way shown below, the subgroup H consists of all cube configurations which show this color pattern H after relabeling.
Pattern H = 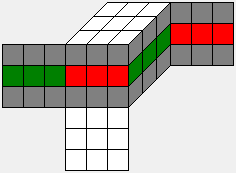
For example, the cube generated by R L' U2 L R'

is from H, because this maneuver does not change the relabeled cube.
Obviously the moves U, D, R2, F2, L2, B2 do not change the relabeled cube, so any sequence of these moves will transform a cube from H to another cube from H. In the second phase of the two-phase-algorithm only these moves are used to solve the cube. It is less obvious that this always works; for example, the cube R L' U2 L R' can be solved by R2 F2 R2 U2 R2 F2 R2 U2 F2, so the quarter-turns R and L are not needed. In general, all possible configurations of H can be generated by the moves U,D,R2,F2,L2,B2, and this provides the group-theoretic definition of the subgroup H as <U,D,R2,F2,L2,B2>.
There are 8! ways to permute the corners without changing the pattern on the relabeled cube, the 4 red/green edges of the middle slice can be permuted in 4! ways, and the remaining 8 edges with the white facelets can be permuted in 8! ways. So H has 8!*8!*4! elements - if we are allowed to disassemble the cube and put it together again. But since Cube positions are instead generated by turning faces, this gives only half of this number. Each face turn is an even permutation, and so H actually consists of only 8!*8!*4! /2 = 19,508,428,800 elements.
Note that it is impossible to twist a corner or flip an edge on the relabeled cube without destroying the color pattern. This is the reason why flips and twists do not contribute to the number of elements of H.
The cosets of H can be visualized in a similar way. Each coset is visualized by a specific color pattern of the relabeled cube.
Pattern X = 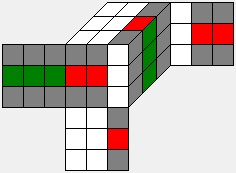
 ,
,  ,
, 
These are examples of cubes belonging to the same coset because the relabeling gives the same pattern X shown above. Formally stated, the coset depicted above is the coset
H*R ={h*R: h from H}.
It is not difficult to see that 2,217,093,120 is the number of possible color patterns (= number of cosets) of the relabeled cube. There are C(12,4) possibilities to place the 4 red-green edges. Flipping an edge or twisting a corner always give a different pattern. Disassembling the cube would give 2^12 * 3^8 ways to combine the flips and twists, but the move constraints allow only 2^11*3^7 ways - it is impossible to flip a single edge or to twist a single corner. So there are C(12,4)*2^11*3^7 = 2,217,093,120 different cosets. But are all these cosets really different concerning the number of moves to solve them?
The color pattern H describing the subgroup H is symmetric concerning the group D4h of the 16 (“dihedral”) symmetries of the cube which preserves the UD-axis. For example, if you turn the color pattern H by 90 degrees around the UD-axis you get,

and if you exchange the colors green and red, you get the pattern H again.
More formally, for a symmetry m of D4h we have m*H*m' = H, where m' is the inverse of m.
Doing the rotation and subsequent color change with the pattern describing the coset H*R.

generates
.
This pattern describes the coset H*F; the situation is the same as with the coset H*R. So if we solve the coset H*R there is no need to solve the coset H*F. We call the cosets H*R and H*F symmetry-equivalent, or simply “equivalent.”
In general, for the coset H*r with r being an arbitrary cube permutation, we have for any element m of D4h that
m*(H*r)*m' = m*(H*m'*m*r)*m' = (m*H*m')*m*r*m' = H*(m*r*m'). This is essentially the coset H*r, just in another spatial orientation.
Because D4h has 16 elements, in most cases 16 cosets are equivalent to each other, i.e. the equivalence class has 16 elements. This is not true for all cosets. The coset H*R for example is equivalent only to H*F, H*L and H*B, while the subgroup H seen as the identity coset is equivalent to no other coset. In both cases the reason is that the cosets have some self-symmetry.
When we reduce the number 2,217,093,120 of H-cosets by the 16 symmetries of D4h it can be shown that there are 138,639,780 essentially different equivalence classes. This is about 2,217,093,120/16, but not exactly. It is a bit more because some equivalence classes have less than 16 elements, as explained above.
But we still can do better than solving all of the 138,639,780 different cosets.
<next >