Permutations and the Facelet Level

If we look at clean the cube, we see 6*9 facelets.

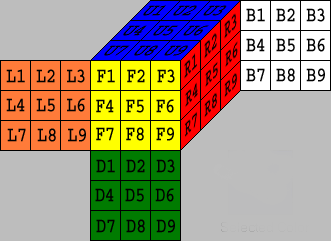
If we apply a move to the cube, the facelets are rearranged. Such a rearrangement is called a permutation.
We use the six letters U, R, F, D, B, L to describe the six 90° clockwise face movements. We use for example F2 to denote a 180° turn and F' to denote a 270° turn, i.e. a 90° turn anti-clockwise of the front face.

If we apply for example a F-move to the cube depicted above we get the following result:

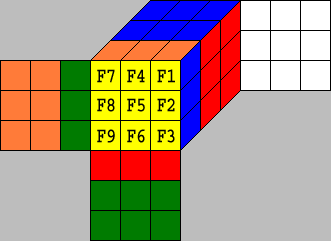
To explain the representation of such permutations, we will only look at the yellow facelets for a moment. There are two possibilities for this representation in the example.

1. F1 is carried to F3 (F1-›F3), F2-›F6, F3-›F9, F4-›F2, F5-›F5, F6-›F8, F7-›F1, F8-›F4, F9-›F7. We can write
   

   F1	F2	F3	F4	F5	F6	F7	F8	F9
   F3	F6	F9	F2	F5	F8	F1	F4	F7

   
   
2. F1 is replaced by F7 (F1‹-F7), F2‹-F4, F3‹-F1, F4‹-F8, F5‹-F5, F6‹-F2, F7‹-F9, F8‹-F6, F9‹-F3. We can write
   

   F1	F2	F3	F4	F5	F6	F7	F8	F9
   F7	F4	F1	F8	F5	F2	F9	F6	F3

Because the first row of the tables is always the same, we can omit this row. So we can write just

(F3,F6,F9,F2,F5,F8,F1,F4,F7) in the is carried to representation or

(F7,F4,F1,F8,F5,F2,F9,F6,F3) in the is replaced by representation.

In most cases we will not use the short form without a table here for the sake of clearness.

We use the first representation on the facelet level, and the second on the cubie level.
In the rest of this chapter the is carried to representation is used.

We are able to define a product of two permutations.

For example

*

=

because for example F1-›F2 by the first permutation and F2-›F6 by the second, so we have F1-›F6 in the product.

The multiplication of permutation has some similarities with the common multiplication with numbers, but there is one big difference: While for example 3*5=5*3, you usually may not exchange the order of the two permutations.

But in the above example, we have

*

=

and this is something different. The multiplication of permutations is not commutative.

Another important term is the inverse permutation.

Consider the F-move

and the permutation

In this case

*

=

This last permutation does nothing at all, so when we multiply a permutation with its inverse, we get the identity permutation I. In fact, in this example the second permutation is the representant of F', so we have F*F' = I, which is quite obvious.
You can check, that also F'*F = I, so in this special case, the multiplication is commutative.

In the file CubeDefs.htm you can see the full definition of the basic moves. For example

F:=(U1,U2,U3,U4,U5,U6,R1,R4,R7,D3,R2,R3,D2,R5,R6,D1,R8,R9,F3,F6,F9,F2,F5,F8,F1,F4,F7,
L3,L6,L9,D4,D5,D6,D7,D8,D9,L1,L2,U9,L4,L5,U8,L7,L8,U7,B1,B2,B3,B4,B5,B6,B7,B8,B9),

written in the short form without a table.

Not only the moves can be viewed as a permutations, every scrambled cubed can be written as a permutation.

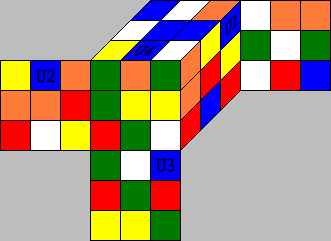
Because U1-›R3, U2-›L2, U3-›D3, U4-›U8,... this cube has the representation (R3,L2,D3,U8,...).

If you solve this cube, you in fact will try to find the inverse permutation of this cube composed as a product of the permutations corresponding to the elementary moves U,U2,U',R,R2,R'..... Recall that the product of a permutation with the inverse gives the identity permutation, and this is the clean cube. The solving algorithm of Cube Explorer tries to find short products for this inverse. For the example in the picture above it finds in a few seconds

R2*L*U2*L2*D*R2*U2*L'*D2*R'*U*B*R'*F2*L2*B2*L2*B2

But representing permutations on the facelet level is not effective for a fast computation. There are two more levels to cope.