Equivalent Cubes and Symmetry

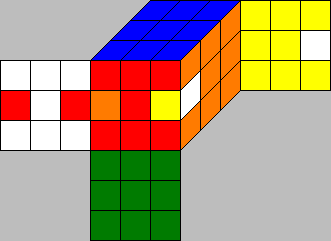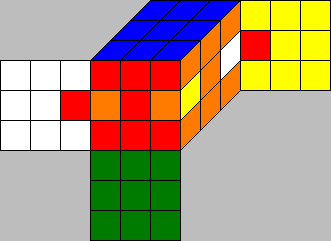
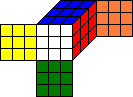
Look at the two cubes above. They look different, but basically they are the same. If you turn the whole cube in the left picture 90 degrees around an axis through the U-center and D-center cubies, you get

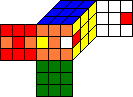this cube, and if you recolor the facelets again so that the color of the F-face is red again etc. you get the cube in the right picture. We call these two cubes equivalent.

Because equivalent cubes have the same structure, the number of moves necessary to solve them is the same.

Defining equivalent cubes with the aid of recoloring of facelets is not really what we want, because we move back to the facelet level. We prefer to define the equivalence on the cubie level with permutations. With S_U4 we denote the 90 degrees turn through the U-center and D-center cubies of the whole cube. Lets denote the permutation which defines the left cube above with A and the permutation for the right cube above with B.

Then we have

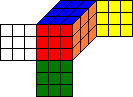S_U4-1

A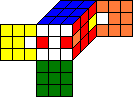

S_U4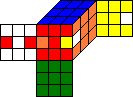

So we have B= S_U4^-1*A*S_U4 in this example. In general, two cube permutations A and B are equivalent, if there is a symmetry S of the cube with

B = S^-1*A*S

For each cube there are up to 48 equivalent cubes, because the cube has 48 symmetries including reflections. In Cube Explorer, these 48 symmetries are generated by four "basic" symmetries:

S_URF3, a 120 degree turn of the cube around an axis through the URF-corner and DBL-corner,
S_F2, a 180 degree turn of the cube around an axis through the F-center and B-center,
S_U4, a 90 degree turn of the cube around an axis through the U-center and the D-center
S_LR2, a reflection at the RL-slice plane.

These basic symmetries are permutations of the corners and permutations of the edges and are described in cubedefs.htm.

Any of the 48 symmetries is uniquely generated by the product

(S_URF3)^x1 * (S_F2)^x2 * (S_U4)^x3 * (S_LR2)^x4

with x1 from 0..2, x2 from 0..1, x3 from 0..3 and x4 from 0..1. This tuple (x1,x2,x3,x4) is mapped to a natural number from 0..47 by

16*x1 + 8*x2 + 2*x3 + x4

In this way each of the symmetries has an associated index from 0..47. With S(i) we denote the symmetry which belongs to the index i.

Two cubes with the permutations A and B are equivalent if and only if there is an i with

S(i)^-1*A*S(i) = B

All cubes which are equivalent, belong to the same equivalence class.

In Cube Explorer the S(i) are implemented in the arrays CornSym and EdgeSym in the unit symmetries.pas