The Two-Phase Algorithm Coordinates

If you turn the faces of a solved cube and do not use the moves R, R', L, L', F, F', B and B' you will only generate a subset of all possible cubes. This subset is denoted by G1 = <U,D,R2,L2,F2,B2>.

A typical representant of G1 looks like this:

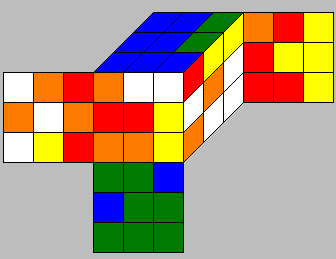
In this subset, the orientations of all corners and all edges are 0. And the four edges in the UD-slice (between the U-face and D-face) stay isolated in that slice.

On the other hand, if the orientations of all corners and all edges is 0, and the four edges of the UD-slice are in their slice, we have an element of G1. This fact is not trivial and relies on the fact that the generators U,D,R2,L2,F2 and B2 generate indeed all elements with this property.
For example

U R2 U R2 D' F2 L2 D' B2 U B2 R2 U2 R2 D2 L2
U2 F2 U2 F2 U2 F2
U2 F2 U2 D2 B2 D2

exchange ULB<–>UBR corners, UR<–>UL edges and BR<–>BL slice edges (for parity reasons together with FR<–>FL) and can be used to construct every possible permutation.

The Two-Phase Algorithm solves the Cube in to steps.

In phase 1, the algorithm looks for maneuvers which will transform a scrambled cube to G1. That is, the orientations of corners and edges have to be constrained and the edges of the UD-slice have to be transferred into that slice. In phase 2 we restore the cube.

There are many different possibilites for maneuvers in phase 1. The algorithm tries different phase 1 maneuvers to find a most possible short overall solution.

In phase 1, any cube is described with three coordinates:

The corner orientation coordinate(0..2186), the edge orientation coordinate (0..2047) and UDSlice coordinate

The UDSlice coordinate is number from 0 to 494 (12*11*10*9/4! - 1) which is determined by the positions of the 4 UDSlice edges. The order of the 4 UDSlice edges within the positions is ignored.

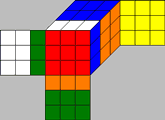
We take the F-move as an example:

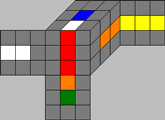
The F-move	UDSlice edges	Ignoring the order

The following function from cubicube.pas implements the computation of this coordinate. The explanation how this works is not obvious and is explained in more detail here. C(n,k) is the binomial coefficient (n choose k).

function CubieCube.UDSliceCoord;
var s: Word; k,n: Integer; occupied: array[0..11] of boolean; ed: Edge;
begin
  for n:= 0 to 11 do occupied[n]:=false;
  for ed:=UR to BR do if PEdge^[ed].e >= FR then occupied[Word(ed)]:=true;
  s:=0; k:=3; n:=11;
  while k>= 0 do
  begin
    if occupied[n] then Dec(k)
    else s:= s + C(n,k);
    Dec(n);
    end;
  Result:= s;
end;

So each cube relevant for phase 1 is described by a coordinate triple (x1,x2,x3), and the triple is (0,0,0) if and only if we have a cube from G1. The problem space of phase 1 has

2187*2048*495 = 2.217.093.120

different states.

In phase 2, any cube is also described with three coordinates:

The corner permutation coordinate (0..40319), the phase 2 edge permutation coordinate (0..40319), and the phase2 UDSlice coordinate (0..23).

The phase 2 triple (0,0,0) belongs to a pristine cube.

The phase 2 edge permutation coordinate is similar to the edge coordinate given in the description of the coordinate level. It is valid only in phase 2.

We have 8! = 40320 possibilities to permute the 8 edges of the U and D face (remember that we only allow 180 degree turns for all faces R, L, F and B).

function CubieCube.Phase2EdgePermCoord: Word;
var i,j: Edge; x,s: Integer;
begin
  x:= 0;
  for i:= DB downto Succ(UR) do
  begin
    s:=0;
    for j:= Pred(i) downto UR do
    begin
      if PEdge^[j].e>PEdge^[i].e then Inc(s);
    end;
      x:= (x+s)*Ord(i);
  end;
  Result:=x;
end;

The phase 2 UDSlice coordinate should have a range from 0..23 because it represents the 4! permutations of the UDSlice edges in their slice. But we use an extension of the UDSlice coordinate instead, which is used in the huge optimal solver anyway and where we also regard the order of the four edges. This "sorted" coordinate has a range from 0 to 11879=12*11*10*9-1. But in phase 2 this coordinate indeed only takes values from 0 to 23.

This is the implementation from cubicube.pas:

function CubieCube.UDSliceSortedCoord: Word;

var j,k,s,x: Integer; i,e: Edge; arr: array[0..3] of Edge;
begin
   j:=0;
  for i:= UR to BR do
  begin
    e:=PEdge^[i].e;
    if (e=FR) or (e=FL) or (e=BL) or (e=BR) then begin arr[j]:= e; Inc(j); end;
  end;

  x:= 0;
  for j:= 3 downto 1 do
  begin
    s:=0;
    for k:= j-1 downto 0 do
    begin
      if arr[k]>arr[j] then Inc(s);
    end;
    x:= (x+s)*j;
  end;
  Result:= UDSliceCoord*24 + x;
end;

The problem space of phase 2 has

40320*40320*24/2 = 19.508.428.800

different states.