Deutsche Version

Inversion of a Dodecahedron 1

Paul Schatz was a German mathematician and inventor with a fable for anthroposophy. One of his discoveries was the inversion of the cube. Stimulated by Paul Schatz's work, several people (among them Klaus Ernhofer, Wolfgang Maas, Immo and Friedeman Sykora) have developed additional inversions of Platonic soldis.

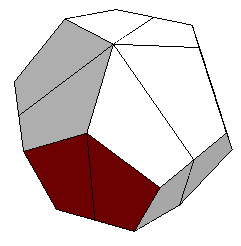
If you cut a dodecahedron into 6 congruent pieces and hinge the parts together, the forced movement is theoretically impossible because at some points of the movement adjacent pieces slightly penetrate each other.


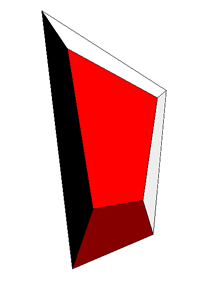
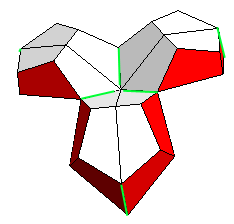
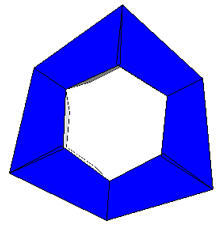
Dodcahedron cut into 6 pieces	A single piece, 4 faces are halfed pentagons	Reassembled, hinges green


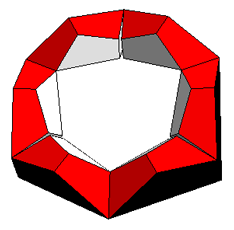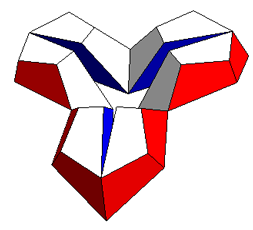
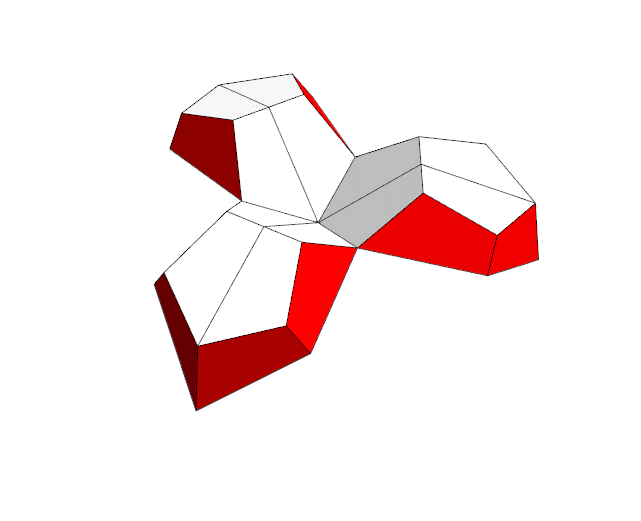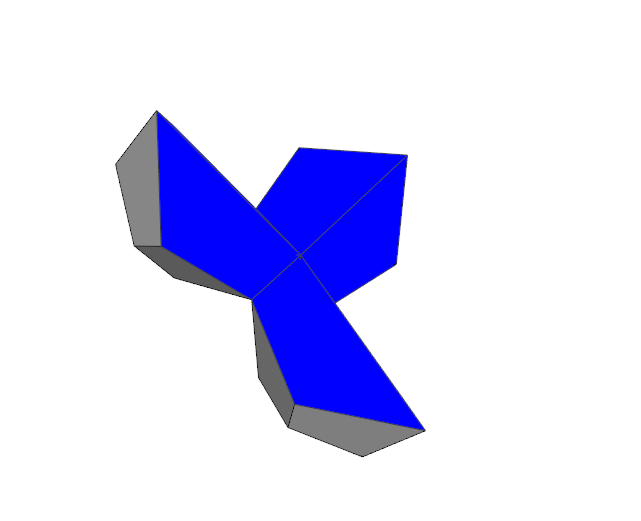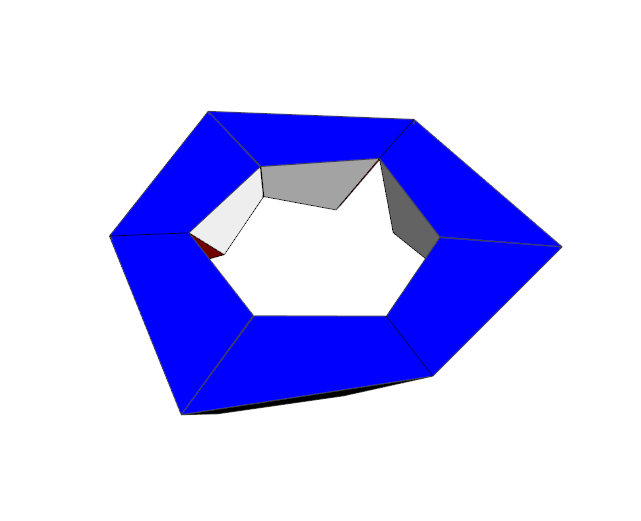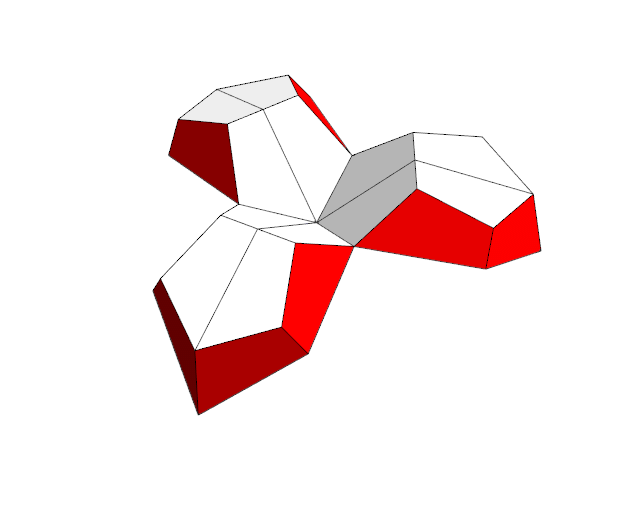
Starting the inversion process		Adjacent faces almost meet


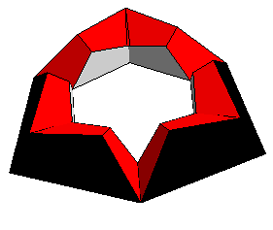
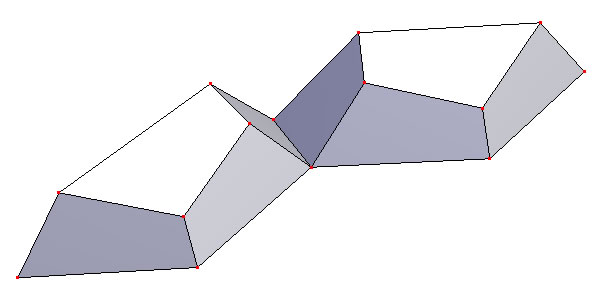
Adjacent faces slightly intersect when the bottom blue faces lie in a plane	The penetration of adjacent pieces is better visible from this side.

The intersecting faces are perpendicular to the blue plane/trapezoids. The angles at the outer long side of the trapezoids are 69.095° and 52.622° with the sum 121.717°. If and only if the sum would be exactly 120° the perpendicular faces would just touch and not penetrate each other.

Btw., using the golden ratio φ, the exact value for 121.717° is π - arctan(φ) in radians.

We try to alter the dodecahedron slightly such that the trapezoids fullfil the 120° condition and the affected faces still stay perpendicular to the trapezoids. We first give an analytic representation of the vertices of the dodecaedron:

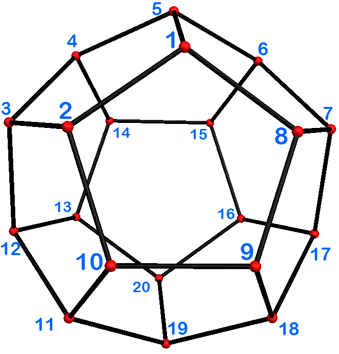
Each of the 20 columns represents the coordinates of the corresponding vertex v(1)..v(20). φ is the golden ratio.

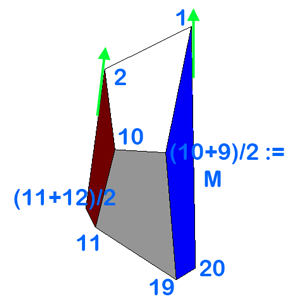
Now we stretch v(1) (and v(20)) by a factor k>1 along edge (1, 20) - the center of edge (1,20) is the origin - and v(2) along the edge which connects the middle between v(11) and v(12) with v(2).

v[[1]] = k v[[1]] (*Mathematica code*)
v[[20]] = k v[[20]]
v[[2]] = v[[2]] + b (v[[2]] - (v[[11]] + v[[12]])/2)

We omit equivalent equations for v(5), v(8), v(13), v(16) and v(19).. The other vertices (3, 4, 6, 7, 9, 10, 11, 12, 14, 15, 17, 18) stay unchanged.
For a given k, b is uniquely determined because we require the new vertices v(1) and v(2) to be coplanar with v(10) and M. We get

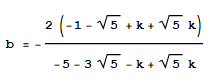
We want to compute k from the 120° requirement for the blue trapezoid.

angle(M,v(1),v(20)) + angle(v(1),v(20),v(19)) = 2π/3

The expressions get really nasty. For the first angle we get after simplification

ArcCos[x1] with
,

for the second

ArcCos[x2] with

So we have to solve the equation ArcCos[x1] + ArcCos[x2] = 2π/3

Using the identity

we can transform this to

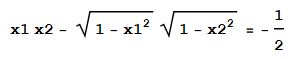
and only after some additional transformations Mathematica was finally able to find the exact solution

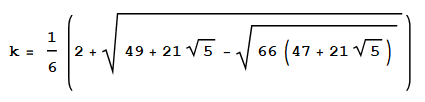
This is about 1.0247447574373178108578826, so the stretching factor is quite small and so is the deviation from the regular dodecahedron. The "pertubed" dodecahedron still has dihedral symmetry D_3d.

Now during the inversion process the adjacent facelets just touch and do not penetrate each other any more. The 6 blue/black trapezoids perfectly fit together when they lie in a plane.

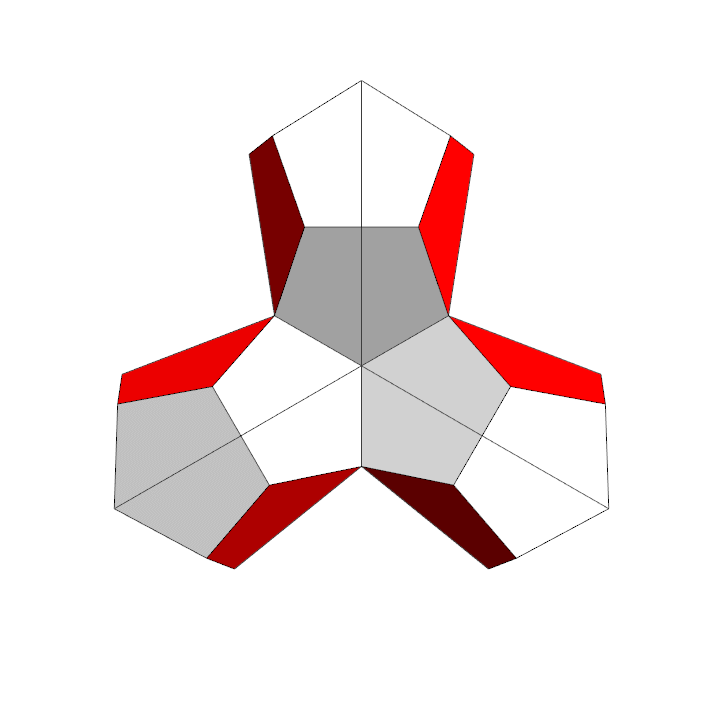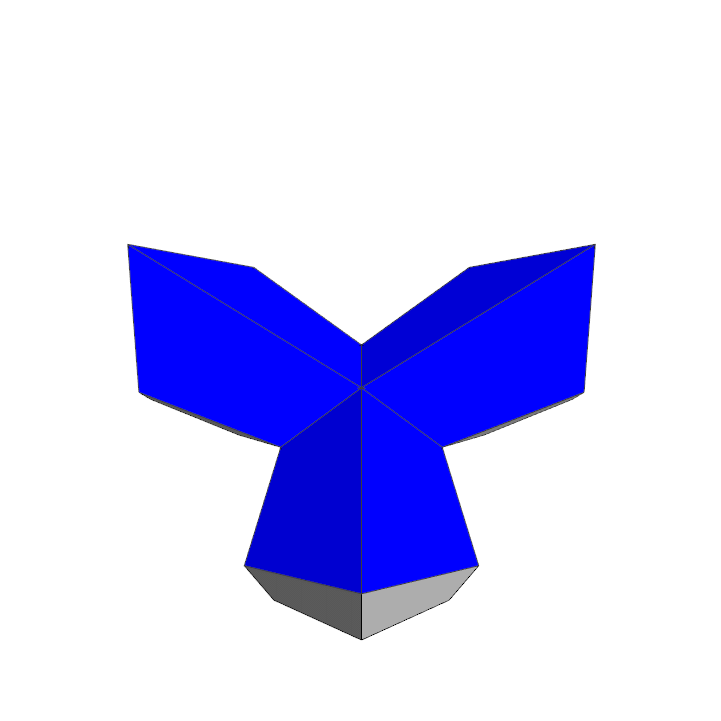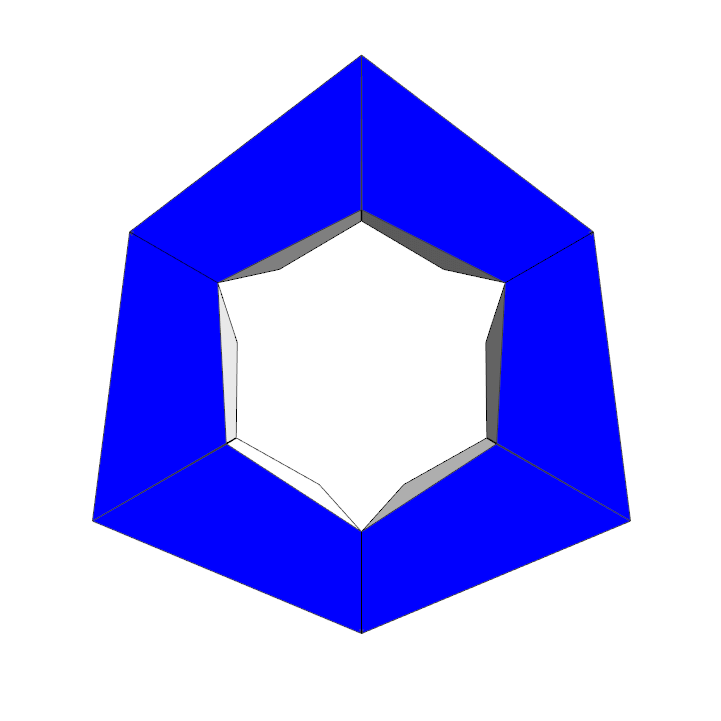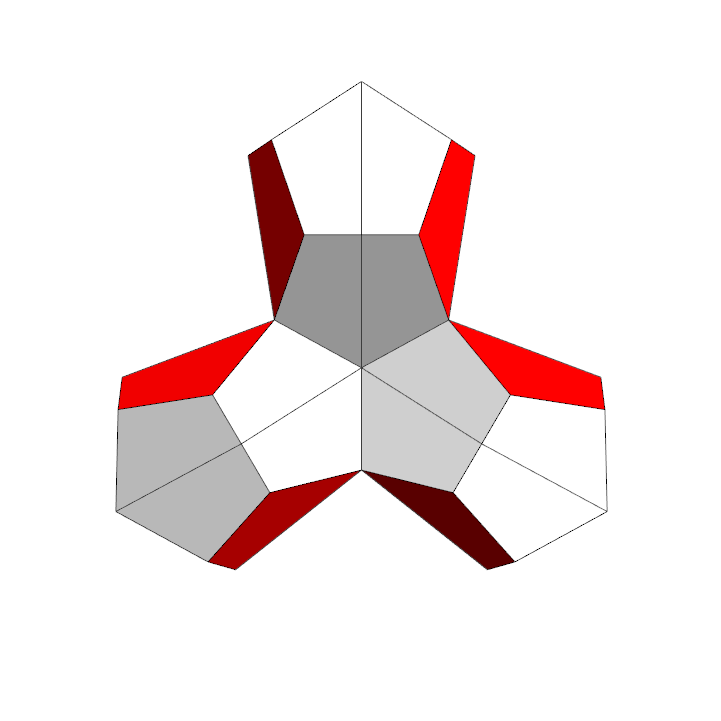
If you want to build a model, here is a pdf file with the net of two hinged pieces. You need three of these nets and some scotch tape to tape the three parts together.

Yet the inversion process is not complete with this model since you have to reassamble the 6 parts before you can start the inversion. We have to remove some parts of our almost-dodecahedron, very similar to what Paul Schatz did with the cube, to get a true inversion.

< Home > < Inversion of a Dodecahedron 2>