Deutsche Version

Inversion of a Dodecahedron 2

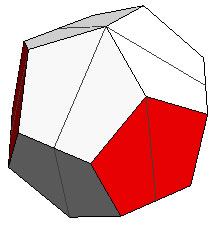
If you start the inversion process of the almost-dodecahedron from the home position of the 6 pieces, the pieces overlap.


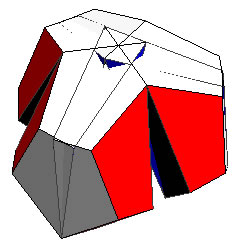
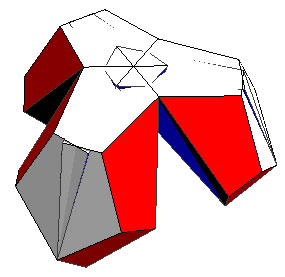
Home position, dihedral angle 0°	dihedral angle 23°	dihedral angle 46°

By applying the methods developed on my kaleidocycle pages I was able to compute the dihedral angle, where the overlap is maximal, it is exactly π - 2 ArcCos[1/16 (1+Sqrt[33])], which is about 49.863°.

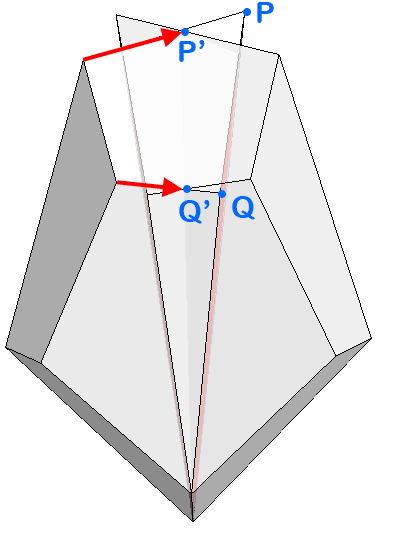
If we move P to P' and Q to Q' the pieces do not overlap but just touch. The lengths of the corresponding edges shrink by the factor 0.5921208162848064 (P-edge) and 0.6479222750007322 (Q-edge). The computation of the exact values is possible but the results are roots of polynomials of degree 8 and cannot be expressed by radicals. Just for completeness, Mathematica gives

Root[4550929-26127318 #1+47818698 #1^2-2301660 #1^3-101954772 #1^4+132286176 #1^5-58036176 #1^6-1881792 #1^7+5645376 #1^8&,3] and
Root[30976-1148928 #1+4108608 #1^2-4522176 #1^3-321408 #1^4+3604176 #1^5-1968300 #1^6+157464 #1^7+59049 #1^8&,4]

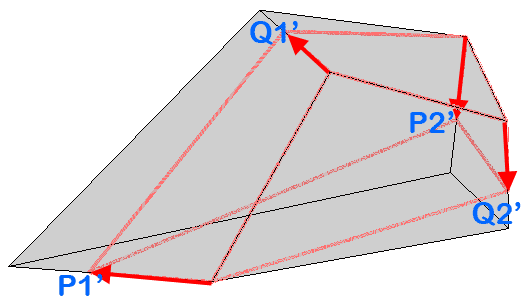
The red wirefram shows what is left if we a apply the cutting process twice. The new piece keeps the twofold rotational symmetry of the original piece and has about 56% of the volume of the original piece.


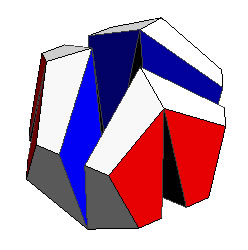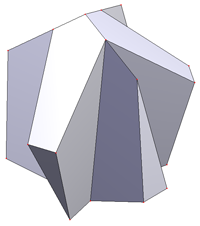The remaining fully invertable chain	Removed part

During a complete inversion cycle there are four positions, where adjacent faces touch each other.

To build a model in analogy to the inversion of the cube of Paul Schatz we dissect the removed part into two identical "Riegel", which look like this from different point of views:

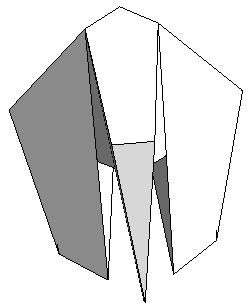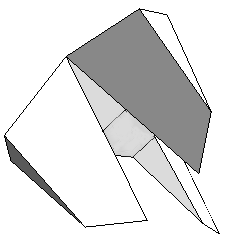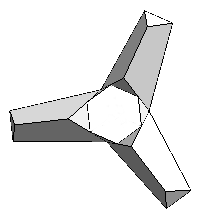For a paper model of a "Riegel" we glue together three identical parts - here also seen from different point of views:

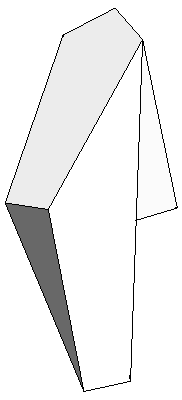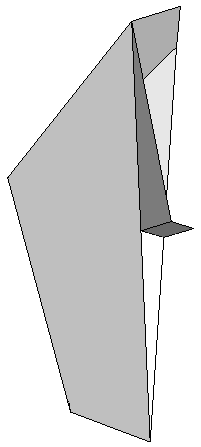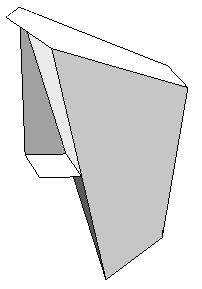Here is the net for one of these parts (omitting the small part of the hexagonal face between the three legs of the Riegel).

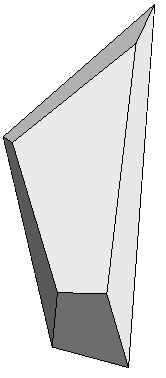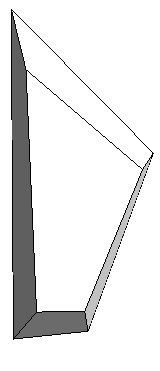The six parts for the "Gürtel" are split into three pieces and its mirror images. The corresponding nets are here and here. For the hinges you can use adhesive tape (Tesafilm), glued from both sides..

Here you can see the resulting model of the inversion of the almost-dodecahedron.

Due to paper thickness the parts do not completely match, but the result still is nice.

< Home > < Inversion of a Dodecahedron 1>