English Version

Die Wurzelspirale

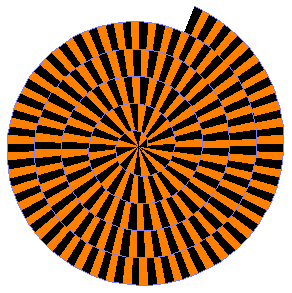
Die Wurzelspirale oder auch Wurzelschnecke wird ausgehend von einem rechtwinkligen Dreieck mit den beiden Kathetenlängen 1 durch das Anfügen weiterer rechtwinkliger Dreiecke erzeugt. Die angefügte Kathete muss dabei immer die Länge 1 haben.

Nach dem Satz des Pythagoras haben die Hypotenusen der erzeugten Dreiecke der Reihe nach die Längenusw. .

Dieses Geogebra-Applet zur Wurzelspirale und dessen Interpolationskurve verwendet Methoden, die im folgenden Text entwickelt werden.

Wenn man die Wurzelspirale als hübsche Anwendung des Satzes von Pythagoras ansieht und sich vielleicht noch fragt, bei welcher Hypotenusenlänge sich die Dreiecke erstmals überschneiden, so kann man hier aufhören. Zeichnet man die Wurzelspirale weiter, so drängen sich allerdings neue Fragen und Vermutungen auf, deren Beantwortung durchaus anspruchsvoll ist.
  1. Die Spiralabstände sehen sehr gleichmäßig aus, und eine numerische Überprüfung lässt vermuten, dass die Abstände sich dem den Wert Pi annähern.
  2. Handelt es sich also nährungsweise um eine Archimedische Spirale, die in Polarkoordinaten durch die Funktionsgleichung r(phi) = a · phi + b dargestellt werden kann?
  3. Wenn ja, welche Werte haben dann die Parameter a und b?
  4. Die erste Umdrehung wird nach 17 Dreiecken vollendet, die zweite nach 54 Dreiecken usw. Gibt es eine Gesetzmäßigkeit für die Folge 17, 54, 110, 186, 281...... ?
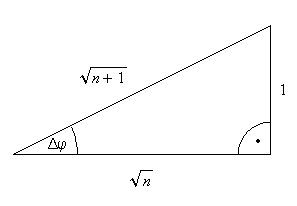Wenn man das dargestellte n-te Dreieck zur Schnecke hinzufügt, beträgt der Winkelzuwachs
= .
Der entsprechende Radienzuwachs ist.
Für große n ist ungefähr und ungefähr halb so groß, nämlich , wie man durch eine Taylorentwicklung leicht zeigt.

Bei einer vollen Umdrehung beträgt der gesamte Winkelzuwachs 2Pi, der Radienzuwachs demnach für große n ungefähr halb so viel, also Pi.

DIese Argumentation "beweist" allerdings nur Punkt 1. Zur genaueren Untersuchung ziehen wir die Eulersche Summenformel heran.

Die Eulersche Summenformel macht eine Aussage über die Summe von Funktionswerten einer hinreichend oft differenzierbaren Funktion:

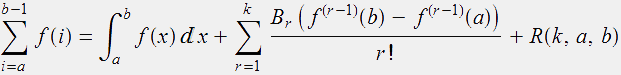         (1)

Dabei sind Br die Bernoulli Zahlen und R(k,a,b) ein Restglied, das von dem beliebig zu wählenden Parameter k >=1 abhängt. Es gilt

R(k,a,b) = 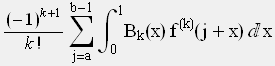                                                                               (2)

wobei Bk(x) das k-te Bernoulli-Polynom darstellt.
Es gilt z.B. B1(x) = x - 1/2, B2(x) = x2 - x + 1/6 und B3(x) = x3 - 3/2 x2 + 1/2 x.

Wir benutzen die Formel (1) jetzt, um den Gesamtwinkel φ(n-1) der ersten n -1 Dreiecke der Wurzelspirale zu bestimmen. Es gilt

φ(n -1) = 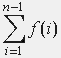, wobei f(x) = , n>=1.

In (1) und (2) wählen wir deshalb a=1 und b=n.
Die zum Gesamtwinkel φ(n -1) gehörige Hypotenuse des n - 1 ten Dreiecks hat dabei die
Länge r = .

Mit Hilfe einer Abschätzung von D.H. Lehmer (American Mathematical Monthly, volume 47, pages 533–538 (1940)), welche zeigt, dass |Bk(x)| in [0,1] im Wesentlichen durch beschränkt ist, lässt sich folgern, dass für f(x) = der Grenzwert von R(k,1,n) in (2) für n → ∞ existiert und

außerdem |R(k,1,∞)| < |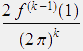| gilt.

Dies bedeutet, dass es eine (von k abhängige) Konstante C gibt, so dass sich φ(n -1) beliebig genau durch

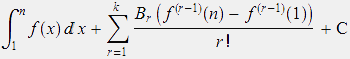                                                                             (3)

annähern lässt, wenn nur n entsprechend groß gewählt wird.

Wir führen jetzt eine Taylorentwicklung von (3) bei n = ∞ bis zur Ordnung g durch und ersetzen durch r. Es lässt sich zeigen, dass die Terme bis zur Ordnung g unabhängig von k sind, solange k≥g.

Mit Mathematica lässt sich diese Berechnung folgendermaßen durchfürhen

g=6;(*Beispiel für Ordnung 6*)
f[x_]:=ArcTan[1/Sqrt[x]]
int1[f_,a_,b_]:=Integrate[f[x],{x,a,b},Assumptions->{a>=1,b>a}]
sum1[f_,a_,b_,k_]:=Sum[BernoulliB[r]/r!*(Derivative[r-1][f][b]-Derivative[r-1][f][a]),{r,1,k}]
FullSimplify[Series[int1[f,1,n]+sum1[f,1,n,g]+C,{n,\[Infinity],g}],Assumptions->n>0];
Normal[%];
FullSimplify[%/.n->r^2,Assumptions:>r>0]//Expand

Bei Entwicklung bis zur Ordnung g erhalten dann mit einer universellen Konstanten K

φ(r)= +.... +O(1/r2g+1)   (4)

Dabei ist r = die Länge der Hypotenuse des n. ten Dreiecks und φ(r) der Gesamtwinkel der ersten n Dreiecke der Wurzelspirale.
Bei der Entwicklung bis zur Ordnung g tritt   2g - 1 als höchster Exponent von r auf. In (4) sind z.B. die Terme bis zur 6. Ordnung zu sehen..

Weiter unten zeigen wir, das K = - 2.157782996659446220929...
E. Hlawka (Gleichverteilung und Quadratwurzelschnecke, Monatsh. Math., 89 (1980) 19-44) bezeichnet diese Konstante K als "Schneckenkonstante".

In 0. ter Näherung erhalten wir φ(r) ≈ K + 2r bzw. r(φ) ≈ φ/2 - K/2.

Damit ist die 2. und 3. Frage beantwortet. Es handelt sich für r → ∞ um eine Archimedische Spirale mit a = 1/2 und b = - K/2.

In 1. ter Näherung erhalten wir φ(r) ≈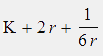

Diese Approximation ist auch für kleine r bereits sehr gut. Die in Polarkoordinaten angegebene Kurve
( r | K+2r+1/(6r) ) ist blau dargestellt..

Zur Berechnung von K benutzen wir, dass sich φ(r) als Winkelsumme der ersten r2 -1 Dreiecke darstellen lässt, φ(r) =.

Damit ergibt sich

K=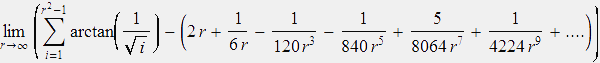

Berücksichtigt man hier als höchste Potenz 1/r199 (Ordnung g=100), so reicht r=1000, um K auf über 500 Dezimalstellen zu berechnen:

-2.1577829966594462209291427868295777235041395986075624551548955508588696
   4679660648149669429894639608987102644546323483961396103365725327148173
   9579479801536750444925748198547939566054940816567775604693493057715919
   0945928100837411349116272651336708202501350168270658030350299970069914
   8589432178461865957563786712790315362413585001910510808455216340245422
   8911282399073166806234610266777983466325557657663517559712701836275736
   9358836893290416857329718037369573784377741773721084014784261501403379
   18331837199800001.......
K lässt sich auch alternativ auch sehr elegant als unendliche Reihe mit Hilfe der Riemannschen Zetafunktion berechnen
( D. Brink, The spiral of Theodorus and sums of zeta-values at the half-integers, The American Mathematical Monthly, Vol. 119, No. 9 (November 2012), pp. 779-786.)

φ(r) = +..........

ist auch eine gute Ausgangsbasis für eine differenzierbaren Fortsetzung für alle reellen r>0, (siehe D. Gronau: The spiral of Theodorus. Amer. Math. Monthly 111, 2004, 230-237).

Während Gronaus Darstellung für φ(r) sehr langsam konvergiert, gibt die Darstellung (4) entwickelt bis zu einer bestimmten Ordnung g eine beliebig genaue Näherung für alle r≥ Rg , wobei Rg von der Ordnung g der Näherung abhängt.

Interessant ist aber auch der Bereich 0< r< 1, und hier ist die Darstellung (4) in dieser Form ungeeignet. Da jedoch gilt

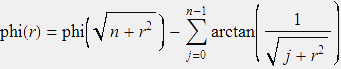
kann man mit geignet groß gewähltem n die Näherung (4) auch für 0< r< 1 benutzen.

In dem Geogebra-Applet werden Terme bis zur Ordnung g=7 verwendet und n=10 benutzt. Dies garantiert einen maximalen Fehler < 10-10 bei φ(r) für alle r>0.

Die folgenden Funktionen sind sehr gute Approximationen sowie untere und obere Schranken für φ(r) mit einem Fehler der Ordnung O(1/r3):

φL(r) =

φU(r) =

Dass dies gilt, sieht man an den Taylorreihen von φL(r) and φU(r) - entwickelt an r = ∞ - und der Vergleich mit Gleichung (4), die den Term 1/(120 r3) enthält:

φL(r) =

φU(r) =

Erstaunlicherweise gilt sogar

φL(r) < φ(r) < φU(r)        for all r≥0,

wie folgende Graphen zeigen:

                

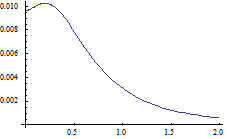
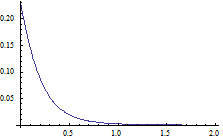
            φ(r) - φL(r)                                                         φU(r) - φ(r)

φL and φU haben einfache Umkehrfunktionen..

Mit a = (φ - K)/2 erhalten wir:

rL(φ) := φU-1(φ) = 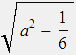, und

rH(φ) := φL-1(φ) = und somit

rL(φ) < r(φ) < rH(φ),      φ > Sqrt[6]/3 + K

Die Folge A072895 der On-Line Encyclopedia of Integer Sequences ist als die kleinste Anzahl von Dreiecken definiert, mit der die Spirale gerade die k-te Drehung vollendet hat. Die Folgenglieder sind

17, 54, 110, 186, 281, 396, 532, 686, 861, 1055, 1269, 1503, 1757, 2030, 2323, 2636, 2968, 3320, 3692, 4084, 4495, 4927, 5377, 5848, 6338.....

Es gilt dann

rL(2kπ) < r(2kπ) < rH(2kπ) und wegen n = r2 -1

Floor[ rL(2kπ)2 ] ≤ A072895(k) ≤ Floor[ rH(2kπ)2 ]

Für alle k≤1 000 000 000 gilt Floor[ rL(2kπ)2 ] = Floor[ rH(2kπ)2 ], also haben wir

A072895(k) = Floor[ rL(2kπ)2 ] = Floor[ (kπ - K/2)2 - 1/6 ] , k≤1 000 000 000

und auch

A072895(k) = Floor[ rH(2kπ)2 ] = Floor[ (kπ - K/2)2 - 1/6 + 1/(12kπ - 6K)2 ], k≤1 000 000 000

 

Folgendes Mathematica Programm berechnet A072895(k) :

a[k_]:=Module[{ a= -K/2 + kπ, b}, b = a2 - 1/6; If [Floor[b]==Floor[b+1/(12 a)2], Floor[b], Undefined]]

Unter der Annahme einer Gleichverteilung  mod 1 ist die Wahrscheinlichkeit für Floor[b] != Floor[b+1/(12 a)2] für jedes k dann 1/(12kπ - 6K)2.

Die Wahrscheinlichkeit, dass a[k] für alle k > 1 000 000 000 definiert ist, lässt sich dann durch

Product [1 - 1/(12kπ - 6K)2,{k,1000000001,∞}] ≈0.99999999999929638

abschätzen.

Mit großer Wahrscheinlichkeit gilt also a[k]= A072895(k) für alle k.

< Home >

© 2022  Herbert Kociemba