Symmetric Patterns

With the Symmetry Editor of Cube Explorer you can search for symmetric cube patterns. We will give some explanation concerning the mathematics of such symmetries here.

A cube has 48 symmetries which build the symmetry group M with 48 elements. A cube symmetry is a geometric transformation, which maps the cube onto itself. If the cube has a pattern, this pattern usually will not map onto itself too.

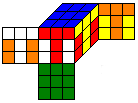	But take for example this cube. If you do 1/4 rotation about the UD-axis, the result is...
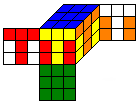	this cube. And if you recolor the facelets again by exchanging yellow with red, red with white, white with orange and orange with yellow you get...
	the first cube again. We call this pattern symmetric with respect to the 1/4 rotation about the UD-axis.

Here is a table of the possible 48 symmetries of the cube

	1/2 rotation around an edge	6 elements
	Reflection through a plane	6 elements
	1/2 rotation around a face	3 elements
	Reflection through a plane	3 elements
	1/4 rotation around a face	2 x 3 elements
	1/4 rotation + reflection through the center	2 x 3 elements
	1/3 rotation around an edge	2 x 4 elements
	Reflection though the center	1 element
+	1/3 rotation + reflection through the center	2 x 4 elements
	Identitiy: do nothing	1 element

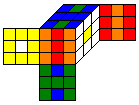There are patterns which only have one of the above symmetries (except the identity), but there also are patterns which have several symmetries. A pattern could be for example symmetric with respect to all three reflections through a plane . This automatically implies the symmetries and . The resulting symmetry type in this example is . An example for a pattern, which has this symmetry is . Altogether there are 33 basically different symmetry types which correspond to certain subgroups of the symmetry group M.

Look at this table to get more information about the 33 symmetry types and cube patterns with these symmetries.