15-Puzzle Optimal Solver

The solved state of the 15-puzzle can be reached from any solvable position within 80 moves or less. Exchanging two arbitrary tiles of a solvable position leads to an unsolvable position. There are 16!/2 = 10,461,394,944,000 different solvable positions.

Korf was able to compute the number of states as a function of the depth in 2005.

depth	states	depth	states
0	1	41	83,099,401,368
1	2	42	115,516,106,664
2	4	43	156,935,291,234
3	10	44	208,207,973,510
4	24	45	269,527,755,972
5	54	46	340,163,141,928
6	107	47	418,170,132,006
7	212	48	500,252,508,256
8	446	49	581,813,416,256
9	946	50	657,076,739,307
10	1,948	51	719,872,287,190
11	3,938	52	763,865,196,269
12	7,808	53	784,195,801,886
13	15,544	54	777,302,007,562
14	30,821	55	742,946,121,222
15	60,842	56	683,025,093,505
16	119,000	57	603,043,436,904
17	231,844	58	509,897,148,964
18	447,342	59	412,039,723,036
19	859,744	60	317,373,604,363
20	1,637,383	61	232,306,415,924
21	3,098,270	62	161,303,043,901
22	5,802,411	63	105,730,020,222
23	10,783,780	64	65,450,375,310
24	19,826,318	65	37,942,606,582
25	36,142,146	66	20,696,691,144
26	65,135,623	67	10,460,286,822
27	116,238,056	68	4,961,671,731
28	204,900,019	69	2,144,789,574
29	357,071,928	70	868,923,831
30	613,926,161	71	311,901,840
31	1,042,022,040	72	104,859,366
32	1,742,855,397	73	29,592,634
33	2,873,077,198	74	7,766,947
34	4,660,800,459	75	1,508,596
35	7,439,530,828	76	272,198
36	11,668,443,776	77	26,638
37	17,976,412,262	78	3,406
38	27,171,347,953	79	70
39	40,271,406,380	80	17
40	58,469,060,820

Korf, R., and Schultze, P. 2005. Large-scale parallel breadth-first search. In Proceedings of the 20th National Conference on Artificial Intelligence (AAAI-05), 1380–1385.

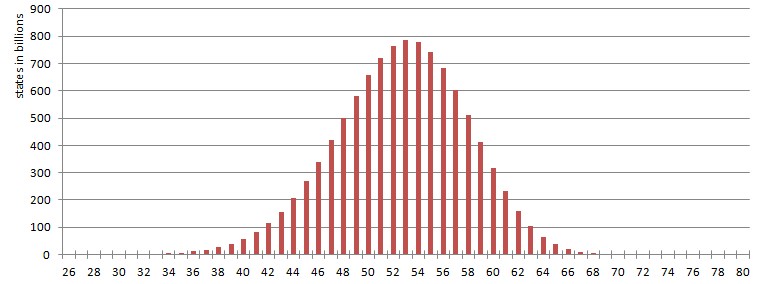
The expected value for the solving length is 52.59.

The 17 positions which need 80 moves are

To find one or all optimal solutions, we do an iterative deepening depth-first search. Using a heuristic which gives a lower estimate of the number of moves to solve the puzzle allows tree pruning (IDA*)

You can choose between several different heuristics:

Manhattan Distance: For each tile the number of grid units between its current location and its goal location are counted and the values for all tiles are summed up. This heuristic is easy to compute but it is not very powerful.
Walking Distance: Considerably more powerful than the Manhattan Distance while not using much memory. Developed by Ken'ichiro Takahashi, see his website for details.
Pattern Databases: The 78 Pattern Database heuristic takes a lot of memory but solves a random instance of the puzzle within a few milliseconds on average. An optimal solution to the 80 moves antipodes takes a few seconds each.
Felner, Ariel, Korf, Richard E., Hanan, Sarit, Additive Pattern Database Heuristics, Journal of Artificial Intelligence Research 22 (2004) 279-318

Generating 1000 random positions led to the following average performance (Intel(R) Core(TM)i7 CPU 920@2.67 GHz, 1 core), in ms/position:

Manhattan Distance: 25600, Walking Distance(WD): 1890, 555-Pattern Database(PDB): 370
555-PDB + WD: 200, 663-PDB: 160, 663-PDB+WD: 120, 78-PDB: 5

I hope the features of the program are almost self-explanatory. You can use drag and drop with the left or right mouse button to swap tiles.

Downloads:

64-bit program (Windows), usually the best choice

32-bit program (Windows)

Borland C++ Sourcecode on GitHub

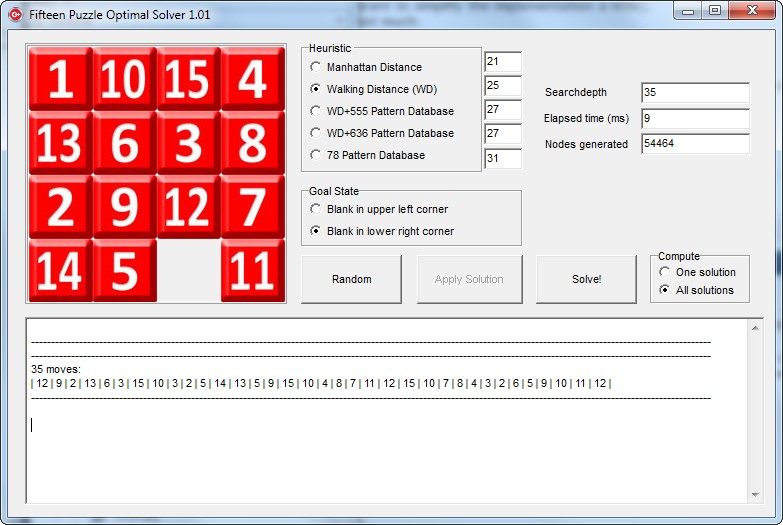
Did you notice that the arrangement of numbers in the 15-puzzle shown above has an interesting property?

The numbers in the rows, columns and both main diagonals all add up to 30.
Such an arrangement is called a Magic Square. There are 7040 different magic squares, but only 3520 of them can be solved with the blank in the lower right corner - as shown at the top of the page. The one shown above is the only one which is solvable within 35 moves and there are no magic squares which are solvable with fewer moves.

A solvable magic square which can be solved with the blank in the lower right corner cannot have the blank in the lower right corner itself. If you color the 4x4 square like a chessboard all possible blank positions of the solvable magic squares have a different color than the lower right corner position. All possible four positions on the diagonal belong to 416 magic squares each, each of the other four positions to 464 magic squares. In total these are exactly the 3520 solvable magic squares.

< Home >