15-Puzzle Optimal Solver
 |
Der Ausganszustand des 15-Puzzles lässt sich von jeder lösbaren Position aus in 80 oder weniger Zügen erreichen. Tauscht man zwei beliebige Kacheln einer lösbaren Position, so entsteht eine nichtlösbare Position. Es gibt 16!/2 = 10.461.394.944.000 verschiedene lösbare Positionen. Korf hat 2005 die Anzahl der Positionen in Abhängigkeit von der minimal benötigten Zugzahl berechnet. |
Tiefe |
Positionen |
Tiefe |
Positionen |
0 |
1 |
41 |
83,099,401,368 |
1 |
2 |
42 |
115,516,106,664 |
2 |
4 |
43 |
156,935,291,234 |
3 |
10 |
44 |
208,207,973,510 |
4 |
24 |
45 |
269,527,755,972 |
5 |
54 |
46 |
340,163,141,928 |
6 |
107 |
47 |
418,170,132,006 |
7 |
212 |
48 |
500,252,508,256 |
8 |
446 |
49 |
581,813,416,256 |
9 |
946 |
50 |
657,076,739,307 |
10 |
1,948 |
51 |
719,872,287,190 |
11 |
3,938 |
52 |
763,865,196,269 |
12 |
7,808 |
53 |
784,195,801,886 |
13 |
15,544 |
54 |
777,302,007,562 |
14 |
30,821 |
55 |
742,946,121,222 |
15 |
60,842 |
56 |
683,025,093,505 |
16 |
119,000 |
57 |
603,043,436,904 |
17 |
231,844 |
58 |
509,897,148,964 |
18 |
447,342 |
59 |
412,039,723,036 |
19 |
859,744 |
60 |
317,373,604,363 |
20 |
1,637,383 |
61 |
232,306,415,924 |
21 |
3,098,270 |
62 |
161,303,043,901 |
22 |
5,802,411 |
63 |
105,730,020,222 |
23 |
10,783,780 |
64 |
65,450,375,310 |
24 |
19,826,318 |
65 |
37,942,606,582 |
25 |
36,142,146 |
66 |
20,696,691,144 |
26 |
65,135,623 |
67 |
10,460,286,822 |
27 |
116,238,056 |
68 |
4,961,671,731 |
28 |
204,900,019 |
69 |
2,144,789,574 |
29 |
357,071,928 |
70 |
868,923,831 |
30 |
613,926,161 |
71 |
311,901,840 |
31 |
1,042,022,040 |
72 |
104,859,366 |
32 |
1,742,855,397 |
73 |
29,592,634 |
33 |
2,873,077,198 |
74 |
7,766,947 |
34 |
4,660,800,459 |
75 |
1,508,596 |
35 |
7,439,530,828 |
76 |
272,198 |
36 |
11,668,443,776 |
77 |
26,638 |
37 |
17,976,412,262 |
78 |
3,406 |
38 |
27,171,347,953 |
79 |
70 |
39 |
40,271,406,380 |
80 |
17 |
40 |
58,469,060,820 |
Korf, R., and Schultze, P. 2005. Large-scale parallel breadth-first search. In Proceedings of the 20th National Conference on Artificial Intelligence (AAAI-05), 1380–1385.
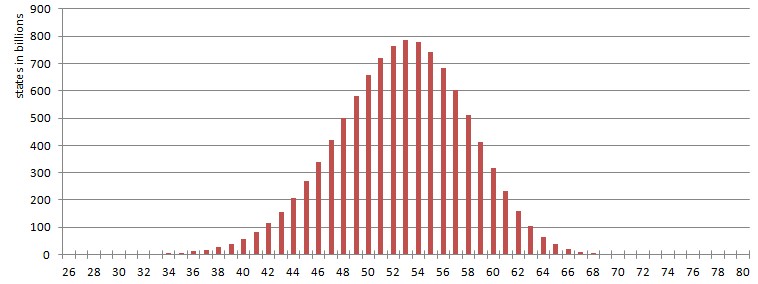
Der Erwartungswert für die kürzest mögliche Lösungslänge ist 52.59.
Die 17 Positionen die 80 Züge benötigen sind:
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
Um eine oder alle optimalen Lösungen zu finden, führen wir eine iterative Tiefensuche durch. Durch die Verwendung einer Heuristik, die eine untere Abschätzung für die von einer Position aus noch benötigte Anzahl von Zügen liefert, lässt sich der Suchbaum beschneiden (IDA*).
Im Programm kann man zwischen verschiedenen Heuristiken auswählen::
- Manhattan Distance: Für jede Kachel wird die Anzahl der Züge berechnet, die eine Kachel von ihrer jetzigen Position zur Zielposition ohne Hindernis benötigt und dann über alle Kacheln summiert.Diese Heuristik ist einfach zu berechnen, aber nicht sehr effektiv.
- Walking Distance: Erheblich leistungsfähiger als die Manhattan Distance und sehr sparsam im Speicherbedarf. Entwickelt von Ken'ichiro Takahashi, mehr Details auf seiner Homepage.
- Pattern Databases: Die 78-Pattern Database Heuristik braucht zwar viel Speicherplatz, benötigt aber in der Regel nur wenige Millisekunden zur Berechnung der optimalen Lösung. Die optimale Lösung für die 17 Antipoden der Länge 80 werden in jeweils wenigen Sekunden berechnet.
Felner, Ariel, Korf, Richard E., Hanan, Sarit, Additive Pattern Database Heuristics, Journal of Artificial Intelligence Research 22 (2004) 279-318
Bei 1000 zufällig erzeugten Positionen ergab sich im Mittel folgende Performance auf einem System mit einer Intel(R) Core(TM)i7 CPU 920@2.67 GHz (1 Kern), Angabe in ms/Position:
Manhattan Distance: 25600, Walking Distance(WD): 1890, 555-Pattern Database(PDB): 370
555-PDB + WD: 200, 663-PDB: 160, 663-PDB+WD: 120, 78-PDB: 5
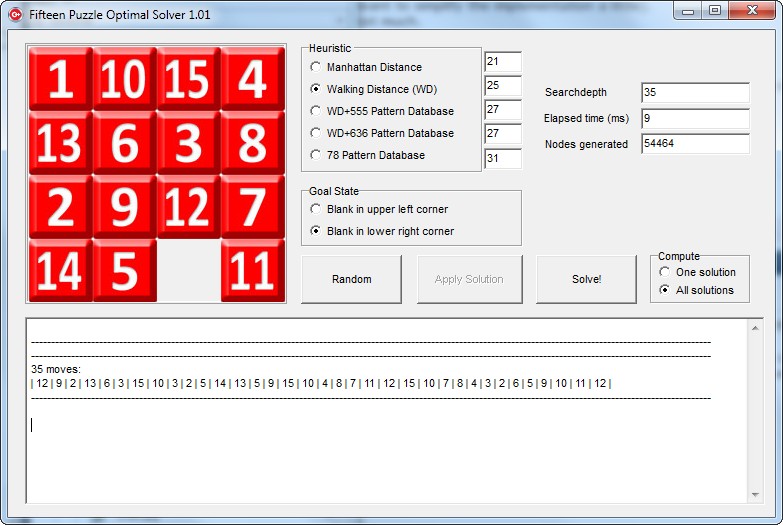
Ich hoffe, dass die Bedienung des Programms selbsterklärend ist. Man kann durch "drag and drop" mit der linken oder rechten Maustaste auch Kacheln vertauschen..
Downloads:
Haben Sie bemerkt, dass die Anordnung der Zahlen in dem oberhalb gezeigten 15-Puzzle eine interessante Eigenschaft aufweist?
DIe Summe der Zahlen in den Zeilen, Spalten und beiden Hauptdiagonalen beträgt jeweils 30. Eine solche Zahlenanordnung heißt Magisches Quadrat. Es gibt 7040 verschiedene magische Quadrate, aber nur 3520 von ihnen lassen sich so lösen, dass der Ausgangszustand wie in dem Puzzle ganz oben besteht, mit dem freien Feld unten rechts. Das gezeigte magische Quadrat ist auch das einzige, das sich in nur 35 Zügen lösen lässt. Es gibt kein anderes magisches Quadrat, das weniger Züge benötigt.
Ein lösbares magisches Quadrat das wie der Ausgangszustand das freie Feld unten rechts hat, gibt es übrigens nicht. Wenn man das 4x4 Quadrat wie ein Schachbrett einfärbt, haben alle möglichen freien Felder der lösbaren magischen Quadrate eine andere Farbe als das Feld unten rechts. Alle vier möglichen freien Felder der Diagonalen gehören zu je 416 magischen Quadraten, die anderen vier Felder zu je 464 magischen Quadraten. Das ergibt insgesamt genau die 3520 lösbaren magischen Quadrate.
< Home >
© 2024 ![]() Herbert
Kociemba
Herbert
Kociemba