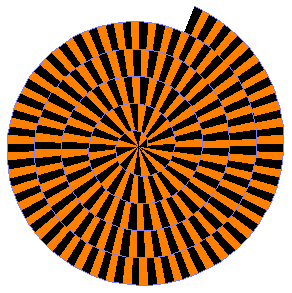
The Spiral of Theodorus

The Spiral of Theodorus starts with an isosceles right triangle with both legs of length 1. More right triangles are added, one leg the hypotenuse of the previous triangle, the other, outside leg, always of length 1. The Pythagorean Theorem tells us that the hypotenuses of these triangles have lengths etc. . This Geogebra Applet dealing with the Spiral of Theodorus and its interpolating curve uses methods developed here.

The Spiral of Theodorus is more than a nice application of the Pythagorean Theorem. If we continue to plot the spiral there are more questions which need more sophisticated mathematics to be answered.

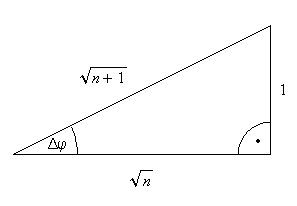If you add the displayed nth tringle, the increase of the angle is = . The corresponding increase of the radius is. For large n is about and about half the size, namely , which can be shown easily with the Taylor series expansion.

For each full revolution, the increase of the angle is 2π, thus the increase of the radius is about half this size, namely π.

This argumentation only shows point 1. To make this more precise, we we use the Euler–Maclaurin formula.

The Euler–Maclaurin formula provides a way to evaluate finite sums using integrals.

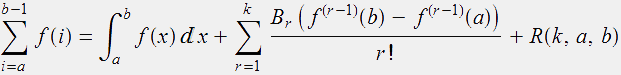          (1)

Here B_r are the Bernoulli numbers and R(k,a,b) a remainder term, which depends on a, b and the parameter k >=1, which can be choosen freely.

We have

R(k,a,b) = 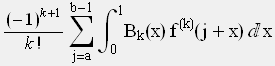                                                                                (2)

B_k(x) is the k-th Bernoulli polynomial.
We have for example B₁(x) = x - 1/2, B₂(x) = x² - x + 1/6 und B₃(x) = x³ - 3/2 x² + 1/2 x.

We use (1) to determine the total angle φ(n-1) of the first n - 1 triangles of the square root spiral. We have

φ(n -1) = 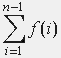, with f(x) = , n>=1.

In (1) and (2) we therefore select a=1 and b=n.
The hypotenuse associated with the total angle φ(n-1) has the length r = .

Using an estimation of D.H. Lehmer (American Mathematical Monthly, volume 47, pages 533–538 (1940)) which shows that |B_k(x)| in [0,1] essentially is limited by , we can conclude that with f(x) = the limit of R(k,1,n) in (2) exists for n → ∞ and moreover we have
|R(k,1,∞)| < || .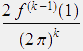

This means that there is a constant C (depending on k) such that φ(n -1) can be approximated with an arbitrary degree of precision by

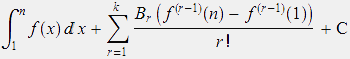                                                                                  (3)

for sufficiently large n.

We now make a Taylor expansion of (3) at n = ∞ to the order g and replace by r. It can be shown that the terms up to order g are independent of k as long as k≥g.

With Mathematica the computation can be performed with the following program:

g=6;(*Example for order 6*)
f[x_]:=ArcTan[1/Sqrt[x]]
int1[f_,a_,b_]:=Integrate[f[x],{x,a,b},Assumptions->{a>=1,b>a}]
sum1[f_,a_,b_,k_]:=Sum[BernoulliB[r]/r!*(Derivative[r-1][f][b]-Derivative[r-1][f][a]),{r,1,k}]
FullSimplify[Series[int1[f,1,n]+sum1[f,1,n,g]+C,{n,\[Infinity],g}],Assumptions->n>0];
Normal[%];
FullSimplify[%/.n->r^2,Assumptions:>r>0]//Expand

Expanding to the order g we then get, with a universal constant K

φ(r)= +.... +O(1/r^2g+1)       (4)

Here r = is the length of the hypotenuse of the n th triangle and φ(r) the corresponding angle sum of the first n triangles..
With an expansion to order g the highest exponent of r is 2g - 1. In (4) for example we see the terms for g = 6.

We show below that K = - 2.157782996659446220929...
E. Hlawka (Gleichverteilung und Quadratwurzelschnecke, Monatsh. Math., 89 (1980) 19-44) describes this constant K as "Schneckenkonstante".

In the zeroth-order approximation we get φ(r) ≈ K + 2r or r(φ) ≈ φ/2 - K/2.

This allows us to answer the second and third question above. For r → ∞ we have an Archimedean Spiral with a = 1/2 and b = - K/2.

In the first-order approximation we get φ(r) ≈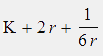

Even for small r this approximation is very good.
The blue curve gives ( r | K+2r+1/(6r) ) in polar coordinates.

To compute K, we observe that φ(r) is the sum of the angles of the first r² -1 triangles,
φ(r) =.

This leads to

K=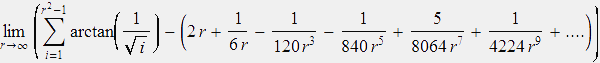

If we take into account 1/r¹⁹⁹ (order g=100) for the highest power of r, r = 1000 suffices to compute K with an accuracy of more than 500 decimal places:

-2.1577829966594462209291427868295777235041395986075624551548955508588696
   4679660648149669429894639608987102644546323483961396103365725327148173
   9579479801536750444925748198547939566054940816567775604693493057715919
   0945928100837411349116272651336708202501350168270658030350299970069914
   8589432178461865957563786712790315362413585001910510808455216340245422
   8911282399073166806234610266777983466325557657663517559712701836275736
   9358836893290416857329718037369573784377741773721084014784261501403379
   18331837199800001.......

Alternatively, K can be calculated elegantly with an infinite series using the Riemann zetafunction
(D. Brink, The spiral of Theodorus and sums of zeta-values at the half-integers, The American Mathematical Monthly, Vol. 119, No. 9 (November 2012), pp. 779-786).

φ(r) = +..........

is also a good starting point for a differentiable continuation for all real r>0 (see D. Gronau: The spiral of Theodorus. Amer. Math. Monthly 111, 2004, 230-237).

While the Gronaus representation for φ(r) converges very slowly, the representation (4) expanded to a certain order g gives an arbitrarily exact approximation for all r≥ R_g, where R_g depends on the order g.

Particulary interesting is the interval 0< r<1, but the representation (4) is inappropriate here.
But we have

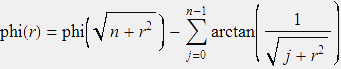
and with a sufficiently large n we can use approximation (4) for 0< r< 1.

In the Geogebra Applet we use terms up to the order g=7 and n=10 . This guarantees an error < 10^-10 for φ(r) for all r>0.

The following functions are very good approximations and lower and upper bounds for φ(r) with an error of order O(1/r³):

φ_L(r) =

φ_U(r) =

To see this, we compare the Taylor series of φ_L(r) and φ_U(r), expanded at r = ∞, with equation (4), which includes the term 1/(120 r³):

φ_L(r) =

φ_U(r) =

Surprisingly we even have

φ_L(r) < φ(r) < φ_U(r)        for all r≥0,

demonstrated by the following graphs:

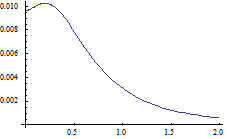
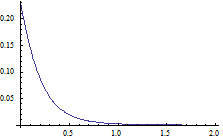
                φ(r) - φ_L(r)                                                         φ_U(r) - φ(r)

φ_L and φ_U have simple inverse functions.

With a = (φ - K)/2 we have:

r_L(φ) := φ_U^-1(φ) = 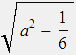, and

r_H(φ) := φ_L^-1(φ) = and hence

r_L(φ) < r(φ) < r_H(φ),      φ > Sqrt[6]/3 + K

Sequence A072895 from the On-Line Encyclopedia of Integer Sequences is defined as the least number of triangles to complete k revolutions. Its elements are

17, 54, 110, 186, 281, 396, 532, 686, 861, 1055, 1269, 1503, 1757, 2030, 2323, 2636, 2968, 3320, 3692, 4084, 4495, 4927, 5377, 5848, 6338.....

We have

r_L(2kπ) < r(2kπ) < r_H(2kπ) and because n = r² -1

Floor[ r_L(2kπ)² ] ≤ A072895(k) ≤ Floor[ r_H(2kπ)² ]

For all k≤1 000 000 000 Floor[ r_L(2kπ)² ] = Floor[ r_H(2kπ)² ] holds, so we have

A072895(k) = Floor[ r_L(2kπ)² ] = Floor[ (kπ - K/2)² - 1/6 ] , k≤1 000 000 000

and also

A072895(k) = Floor[ r_H(2kπ)² ] = Floor[ (kπ - K/2)² - 1/6 + 1/(12kπ - 6K)² ], k≤1 000 000 000

The following Mathematica Program computes A072895(k) :

a[k_]:=Module[{ a= -K/2 + kπ, b}, b = a² - 1/6; If [Floor[b]==Floor[b+1/(12 a)²], Floor[b], Undefined]]

Under the assumption of an equidistribution mod 1, the probability that Floor[b] != Floor[b+1/(12 a)²] is 1/(12kπ - 6K)² for each k.

The probability that a[k] is defined for all k > 1 000 000 000 hence is

Product [1 - 1/(12kπ - 6K)²,{k,1000000001,∞}] ≈0.99999999999929638

With high probability, therefore, a[k] = A072895(k) for all k.

© 2022   Herbert Kociemba