The Cubie Level

On the cubie level, the objects we permute are not the facelets, but the 12 edges and the 8 corners.

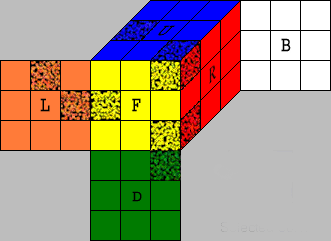
In the picture above, the URF-corner, ther DFR-corner, the FL-edge and the UL-edge are marked.
The corners are named URF, UFL, ULB, UBR, DFR, DLF, DBL and DRB. The edges are named UR, UF, UL, UB, DR ,DF, DL, DB, FR, FL, BL and BR.

On the cubie level it is not possible to represent a move or a scrambled cube by a simple permutation, because the corners can be twisted and the edges can be flipped.

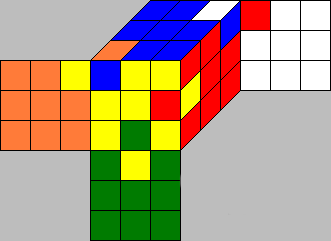
Here the cubies are in their home-positions, but the orientations have changed. The UFL-corner ist twisted clockwise, the UBR-corner is twisted anti-clockwise and the DF-edge and the FR-edge are flipped.

If the corners or edges are not in their home positions, there are many ways to define the orientations of the cubies. But for the Two-Phase-Algorithm, the following definiton is necessary.

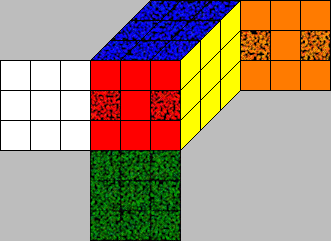
The marked facelets on the clean cube are the reference for the orientation. If a cubie moves to a different position and the reference facelet of this cubie matches with one of the reference facelets of the clean cube we define the orientation to be 0. Else the orientation is 1 for edges and we call the edge flipped and 1, or 2 for corners - we call the corner twisted clockwise or twisted anticlockwise.

When the orientations of all edges and corners are 0 the used reference frame has the property that 10 of the 18 possible cube moves do not change these orientations. This is a crucial property which is needed for the solving algorithm to work.

In the picture, the corner at the place URF is twisted clockwise relative to the reference facelet on the clean cube, also the corner at the place DLF. The corners at the places UFL and DFR are twisted anti-clockwise. The edges sitting in the UF, DF, FL and FR positions are flipped.

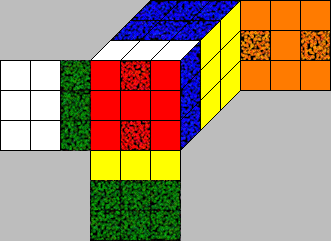The F-move

We use the "is replaced by" representation to write the permutations on the Cubie Level. In the above example: URF is replaced by UFL(URF‹-UFL), UFL‹-DLF, ULB ‹-ULB, UBR‹-UBR, DFR‹-URF, DLF‹-DFR, DBL ‹-DBL, DRB‹-DRB. We write

in this case for the permutation of the corners.

But we have also to keep track of the changes of the orientations, and so we write

F =

We use "0" if the twist does not change, "1" for a clockwise twist and "2" for a anti-clockwise twist. In this way we can add orientations in a simple way. If we do for example two anti-clockwise twist, the resulting twist is 2+2=4, and because 4 = 1 mod 3 the result is a clockwise twist. Take a look at CubeDefs.htm for the definition of the basic moves.

The permutation of the edges is defined similar, with "1" for the orientation of a flipped edge and "0" for an unflipped edge.

We also need a notation to describe a permutation without using a table.
For the F-move above we write for example

F(URF).c = UFL
F(URF).o = 1
F(UFL).c = DLF
F(UFL).o = 2
etc.

We use another move

R =

to show how to define the product F*R of these two permutations including the orientations.

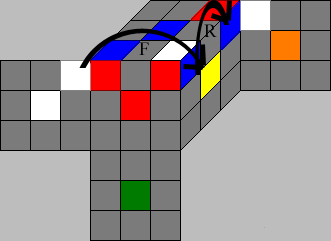F*R applied to the UFL-corner

F(URF).c = UFL and F(URF).o = 1 in the table above tells us that the corner at position URF is replaced by the corner at position UFL and that the orientation of the corner which moves to the position URF is increased by 1 when performing a F-move.
R(UBR).c = URF and R(UBR).o= 1 tells us, that the corner at position UBR is replaced by the corner at position URF and the orientation increases by 1 when performing a R-move.

So when performing F*R we have URF‹-UFL by the F-move and then UBR‹-URF by the R-move, which in the result is UBR‹-UFL. So as result we have the (F*R)(UBR).c = UFL. This means that (F*R)(UBR).c = F(R(UBR).c).c.

The behavior of the orientation is more difficult to understand. F tells us thar F(URF).o=1 when URF‹-UFL. This means, the orientation of the corner which moves from position UFL to position URF increases by 1. This orientation adds to the change of the orientation of the corner which moves from the URF to the UBR position ( UBR‹-URF) by the following R-move. So we have F(URF).o+R(UBR).o for the resulting orientation change at position UBR, and because URF= R(UBR).c we have (F*R)(UBR).o=F(R(UBR).c).o+R(UBR).o.

In general, for two permutations A and B and for any corner position x we have

(A*B)(x).c=A(B(x).c).c

and

(A*B)(x).o=A(B(x).c).o+B(x).o

The same principle holds for the edge permutations. See CubeDefs.htm for the implementation of the multiplication routines.

If we also want to include the case of reflections, which we need if we apply symmetries of the cube, thing are a bit more complicated with the orientations of the corners. Instead of adding modulo 3 in the second equation above, which can be interpreted as a group operation in the cyclic group C₃, we then work in the dihedral group D₃. We describe the three extra elements in this group with the numbers 3, 4, and 5.