Two-Phase-Algorithm and God's Algorithm:

God's number is 20
The algorithm which gives an optimal solution in the sense that there is no shorter solution is called God's algorithm. There are cube positions (for example the superflip which flips all 12 edges), which are known to have a shortest maneuver length of 20 moves to be solved. After 30 years it has finally been shown in July 2010, that all cube positions can be solved within 20 moves or less.

God's Number is 20

An overview is given on the webpage http://cube20.org/.

Our proof was published in SIAM Journal on Discrete Mathematics (Volume 27, Issue 2).

I tried to make a few webpages, which give more detailed information about the proof without being too technical. Some subgroups and their cosets play an important role here, and if you have some basic knowlege of group theory and combinatorics you should be able to follow the train of thoughts.

  1. The subgroup H and its cosets
  2. The subgroup Q and its cosets
  3. Solving a reduced set cover problem
  4. A fast coset solver

The Two-Phase-Algorithm gives near optimal solutions

I generated 1 million random cubes on a 3 GHz Pentium 4 PC, trying to find a cube which was not solvable within 20 moves with the Two-Phase-Algorithm.

But the Two-Phase-Algorithm solved all generated random positions within 20 moves. More precisely, it solved about 30000 random cubes per hour and the final distribution of the maneuver length was:
13: 4, 14: 18, 15: 81, 16: 609, 17: 3893, 18: 23411, 19: 141366, 20: 830618.

Nevertheless the computation of God's number showed, that there some very rare positions which are quite hard to solve within 20 moves with the two-phase algorithm, for example the cube generated by the maneuver
L R2 U2 B' D2 L D2 F' U' R U2 L' F' D' R' B2 D2 R' U' F2 . On my machine this one takes 16 minutes (in triple search mode).

Optimal Cube Solver

In 2009 I used Cube Explorer 4.64s and an Intel Core i7 920 CPU machine (Vista 64 bit with 6 GB of RAM) to solve 100000 random positions optimally in parallel on 8 cores (4 physical and 4 virtual cores).



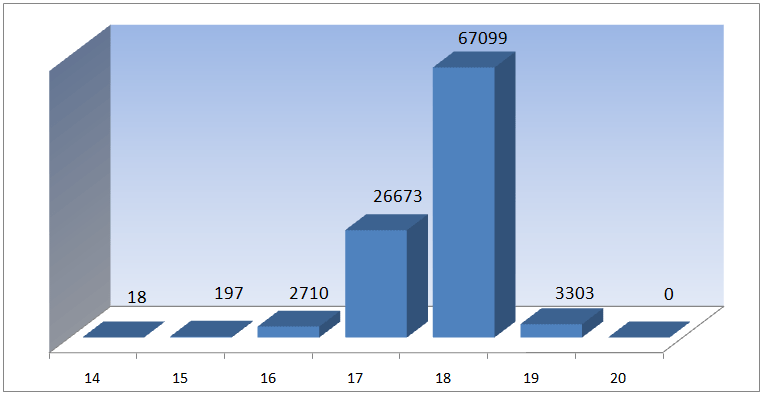
On average the program solved about 7000 cubes/day ! In this sense Cube Explorer's implementation of God's Algorithm does a decent job.. The average optimal solving length is ~17.7 . If you want to download the 100000 optimally solved cubes for some reason, you can do this here.

In January 2010 Tomas Rokicki even solved 1 million random cubes optimally and got the following distribution, which is very close to the distribution I got:

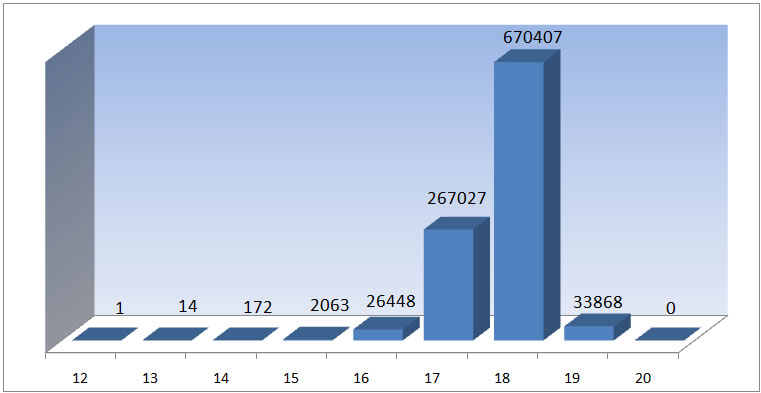
As you can see, it is unlikely to find a cube position which really needs 20 moves by random. Presumably the chance is less than 10-11, see here for details.

The first cube proved in 1995 to need 20 moves was the superflip, a highly symmetric cube position.

Theoretical Probability Distribution

Though we now know, that all positions can be solved within 20 moves, the theoretical distribution for the maneuver length of God's Algorithm for Rubiks Cube is only known for maneuver lengths less than 16.

Because there are 1, 18, 243, 3240, 43239, 574908, 7618438, 100803036,1332343288, 17596479795, 232248063316, 3063288809012, 40374425656248, 531653418284628, 6989320578825358, 91365146187124313 positions which have a shortest maneuver length of n moves for n = 0 to 15 (see sequence A080601 in the On-Line Encyclopedia of Integer Sequences) and there are 43252003274489856000 different cube positions, we get for the probability P to solve a random cube optimally in n moves:

Maneuver Length n
Probability P
Branching Factor B
0
2.31203 *10-20
18
1
4.16166*10-19
13.5
2
5.61824*10-18
13.3333
3
7.49098*10-17
13.3454
4
9.99699*10-16
13.2961
5
1.32921*10-14
13.2516
6
1.76141*10-13
13.2315
7
2.3306*10-12
13.2173
8
3.08042*10-11
13.2072
9
4.06836*10-10
13.1986
10
5.36965*10-9
13.1897
11
7.08242×10-8
13.1801
12
9.33469*10-7
13.1681
13
1.22920*10-5
13.1464
14
1.61595*10-4
13.0721
15
0.0021124
~12.8 (simulation)
16
simulation result: ~0.0264 ±0.0003*
~10.1 (simulation)
17
simulation result: ~0.267 ±0.0009*
~2.51 (simulation)
18
simulation result: ~0.6704 ±0.0009*
~0.051 (simulation)
19
simulation result: ~0.03387 ±0.0004*
probably below 3*10-10
20
P>0, but probably below 10-11
0
>20
0
-
*: 95% confidence interval

Important milestones on the path towards God's number

Phase 1 of the Two-Phase-Algorithm needs at most 12 moves and phase 2 needs at most 18 moves. Michael Reid showed in 1995, that the 18 moves case for phase 2 always can be avoided. So all cubes can be solved within 29 moves.

Gene Cooperman and Dan Kunkle claim in this paper (2007) to have proven that 26 moves suffice, but there is yet a gap in the paper. This gap seems to be fixed meanwhile (August 2007, see Kunkles comment in the Domain of the Cube Forum but the corrected paper is not available.

Silviu Radu proved in this paper (also 2007) that 27 moves suffice.

In May 2008 Tomas Rokicki proved, that 23 moves suffice, analyzing more than 200000 cosets of the phase 2 subgroup of the Two-Phase-Algorithm (Domain of the Cube Forum). The method is similar to the method Rokicki describes in this paper (also 2008) for 25 moves.

In August 2008 Tomas Rokicki reduced the upper bound to 22 moves after having analyzed 1.28 million cosets within 50 core-years of CPU time (Domain of the Cube Forum). See this well written paper for details.

In July 2010 Morley Davidson, John Dethridge, Tomas Rokicki and me proved that God's Number for the Cube is exactly 20.

© 2018  Herbert Kociemba